一級建築士試験＿＜構造＞計算問題を解ける人の脳内を解説（３）

一級建築士試験の構造分野の力学計算問題について、

「なんでそんな風に考えることができるのか？」

に焦点を当てて、「考え方」にフォーカスして、色んな問題へ応用できるように解説します。

問題

解ける人の頭の中

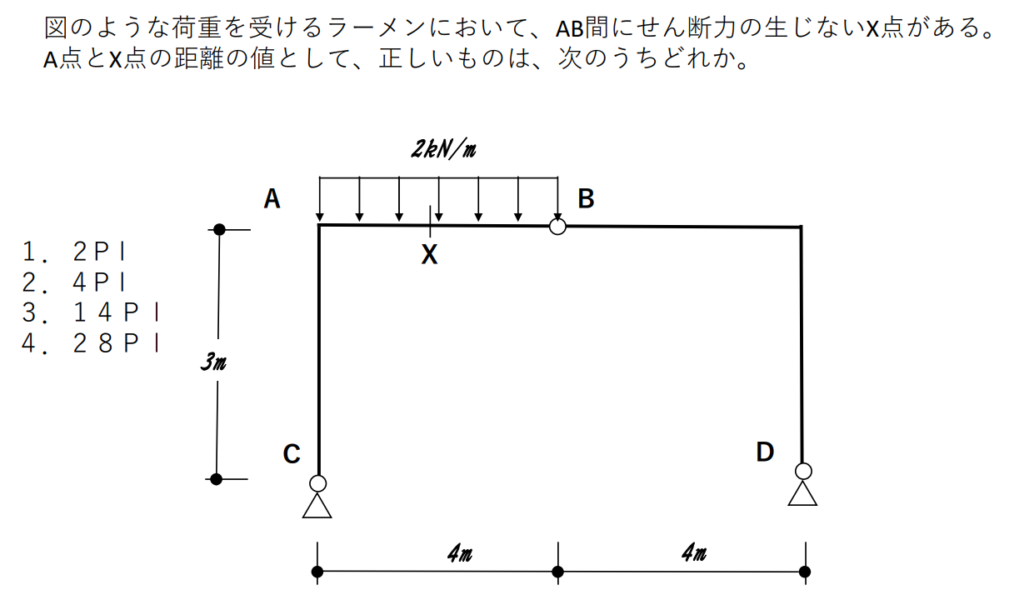
まず、問題を見ると、AB間のどこかにある、せん断力の生じないＸ点のＡ点からの距離の数値を出す問題と分かります。

「具体的な数値を計算で出す方式ということは、方程式を解く必要があるな。じゃあ、方程式は２つくらいは必要そうだな」と考えます。

今回は曲げモーメントではなくて、せん断力が０というのがキーポイントなんだな。

曲げモーメントが０というのは、その点周りのモーメントで方程式を立てるから、せん断力でも同じかな？

一旦、最後の方程式がどうなりそうかだけ考えてみよう。

（最初の考え方が違っても答えに辿りつけることを示せるように、ここから少し敢えて遠回り思考したいと思います。）

せん断力が０になる点を示せばいいわけだから、モーメントの釣り合いを考えれば良いのかな？

どこかでモーメントのつり合いを考えるために、図を２つに分けてみよう。

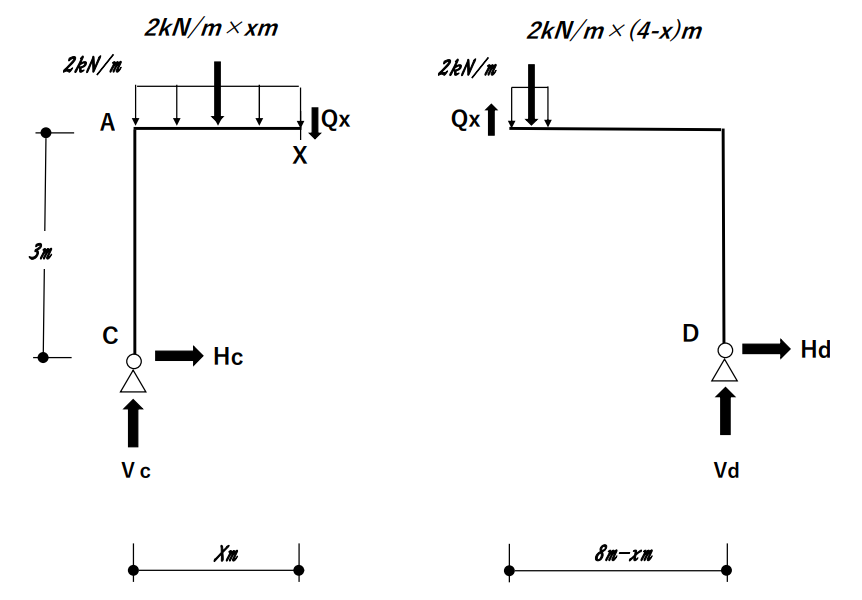
左と右のどちらがいいだろうか？

右の方はXに関する数値にマイナスがついて、色々と計算するのがめんどくさいのが目に見えているので、左側で考えてみよう。

まず、いつものようにモーメントのつり合い式を考えてみよう。

今回モーメントが０になる点は、C点周りだけだから、

$Qx × x + 2x × x/2 = 0$

あれ？これだと２次方程式になってしまう。

２次方程式は2つの方程式がないと解けないけど、モーメントが０になる点は１つだからつり合い式がこれ以上作れないぞ。。

そうだ！つり合い式は、モーメントだけじゃなくて、ものが動いていないことに基づいて、

上下・左右方向の力のつり合い式がたてられるはずだ。

$Vc－２ｘ－Qx＝０$

ここでQx=0だから、Vc＝２xということだ。

じゃあ、Vcがわかればｘが求まるぞ。

Vcを求めるために、全体の絵をもう一度見て、D点周りのモーメントつり合い式を考えてみよう。

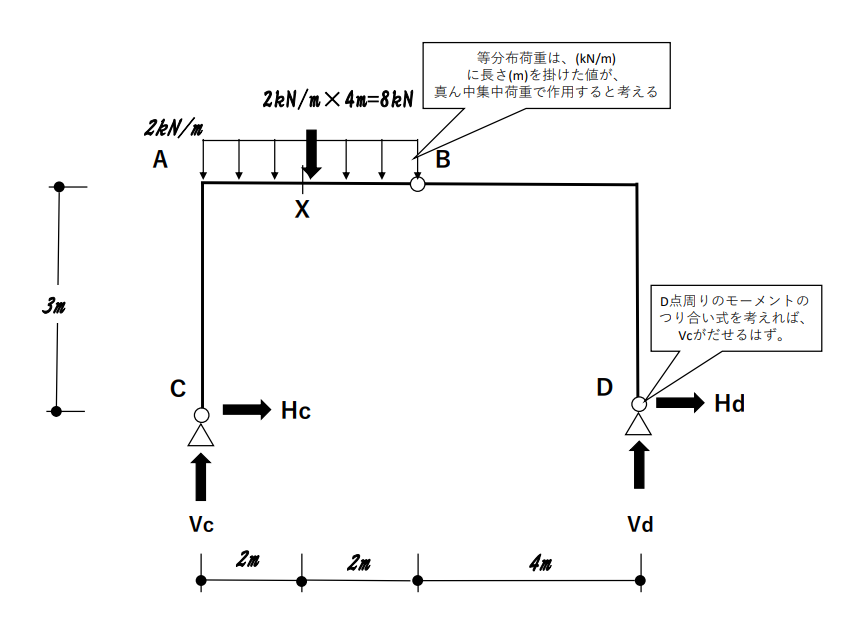
$Vc×8-2×４×6=0$

$Vc=6(kN)$

$Vc=2x=6$ だから

できたー！！

$x=3$

今回のポイント

今回のポイントを振り返ると、やはりモーメントのつり合いではなく、

上下方向の力のつり合い式を立てることができるかということでしょう。

最初はモーメントが０になる点を探して、モーメントのつり合い式を立てるのが定石です。

ただ、今回のように、モーメントのつり合い式が2次方程式になってしまい、直接解けない場合は、

一度落ち着ていて、問題の条件から他につり合い式を立てることができないか考えてみましょう。

試験問題は基本的に「物体は動かない」状態ですので、「力のつり合い式」は必ず成立しています。

その点を頭の片隅に入れておけば、今後の問題でも応用が利きます。